Nous effectuons ensuite un développement au deuxième ordre
de la fonction Q, où nous vérifions facilement que
le terme quadratique est :
(1) ![]()
que nous pouvons diagonaliser sous la forme Q=Uf
UT. Ce changement de base est appliqué au poids spectrale,
de sorte que
(2) 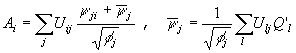
Ce changement de base nous permet d'écrire ![]() .
Nous pouvons donc minimiser la norme du vecteur y
avec certaines contraintes de positivité.
.
Nous pouvons donc minimiser la norme du vecteur y
avec certaines contraintes de positivité.